Sen(Qian)’s Memo

https://openreview.net/pdf?id=QwvaqV48fB

cost-sensitiveは、Negative例がないので、過分に識別境界はNegative寄りになってしまう。sample-selectionでは、初期段階の選択ミスが後々に大きく響く。

いずれにせよ、どのようなPU Learningの手法において、Positiveデータを何回もサンプリングをすることによって、Negativeに偏りすぎる(Cost-Sensitive)問題を解決できる。(クラス事前確率を使って) つまり、モデルを1つのPositive, Unlabeledのセットから選び出すことは偏る。なので、何回もサンプリングしてその都度(毎epochかな？)訓練を施すという手法を使う。

ただし、この手法を使うと最初の訓練のうちは非常にうまくいくけど、すぐにoverfitting?して性能が低くなってしまう。`Resamplingでも、Negative Assumptionは解決できなかったのである。

ここで、Resamplingの手法で、ちょうどいいタイミングで学習を打ち切ることが重要。ここで、Temporal Point Process(TPP)という、包括的な視点をとって、既存の値に基づいて損失を検査したり、信頼度の閾値を調整する手法するらしい。トレンドは「増加」、「減少」、「変化なし」に分けられる。そのうえ、Trend Scoreという傾向を定式化するものを提案した。

やったことは以下の3つ。

• resamplingの良い戦略を提供した。
• Trend Scoreという傾向について定量的に分析するものを定義した。Fisher’s Natural Breakを修正したものを使ったらしい。

サンプルは $\mathbf{x}$であり、Ground-Truthのラベルは $y \in 0, 1$で0はNegative、1はPositiveである。 $y=1$のサンプルの一部がPositiveとして扱われて、集合 $P$に、それ以外(すべてのNegativeと $P$に入らなかったPositive)は $U$になる。

imbalanced, biasedなデータに有効な手法。ここでは、独立に $b$回サンプリングして、各バッチ？の損失の平均を全体の損失としてとると考える。訓練する際は、imbalanceだとやりづらいので、真の割合はそうでないことを織り込んだうえで、 $|B_P| = |B_U|$となるように毎回のバッチ？をとる。この手法で、Labeled Dataを強調することができる。

このように、同じデータに対して何epochも学習するのではなく、それぞれ違うデータセット(同じ分布からの取得)から学習を行うことで、いい性能が得られる。しかし、iterを増やすとNegative Assumption(Cost-sensitive特有の結局はUnlabeledを重み付きのNegativeのように見なしての学習なので、識別境界がNegativeに行きがちでありfalse negativeが多発する現象)が悪化してしまう。これを防ぎたくてResamplingやっているのに結局こうなっちゃうんだ。

いろいろData Augumentationも試したけどうまくいかなかったよ。

この問題を解決するべく、Noisy Labelとみなしたうえでの研究では何かしらの閾値を設けてクリアしたデータだけを使って訓練する手法がある。📄2019-ICML-[PUbN] Classification from Positive, Unlabeled and Biased Negative Data これとか？

だけど、どうやらResamplingするときにPositive側とUnlabeled側の損失の低下が違う(Unlabeledの学習は遅く、Positiveの学習は早い)、そこらへんでも難しい学習となる。

DNNで学習すると非常に高い表現能力で、Nergative Assumptionはさらに激しくなる。なので、適宜なところで打ち切って過学習を防ぐことが重要。

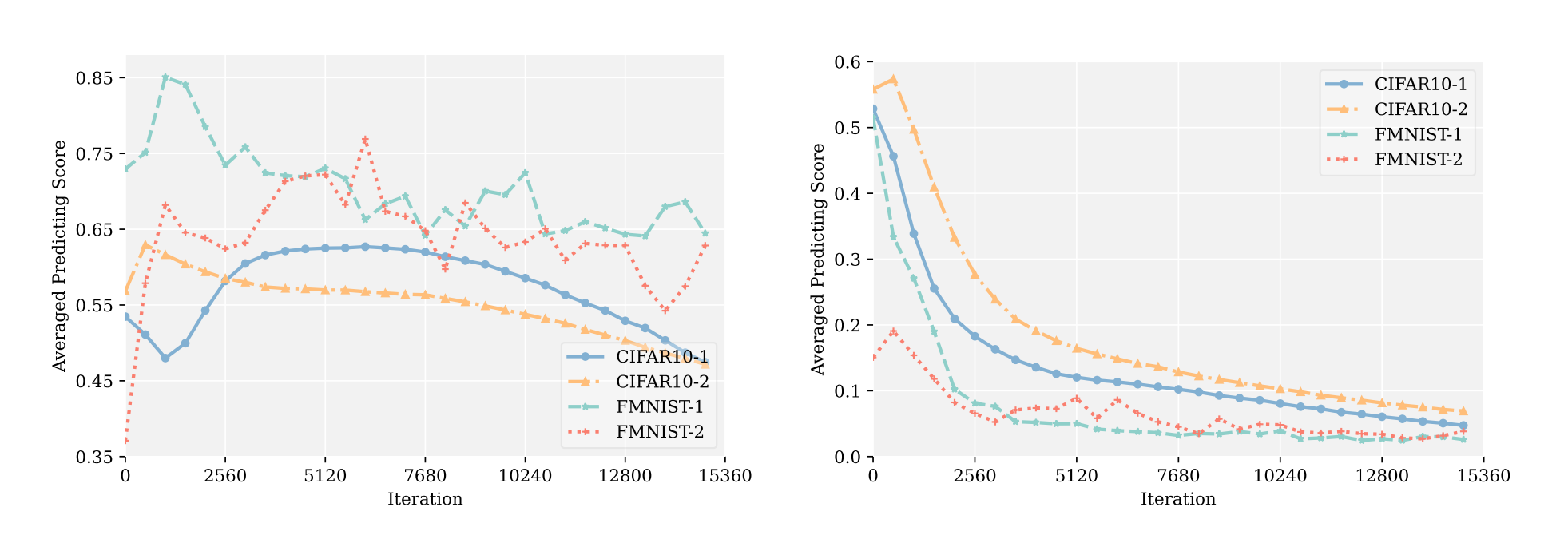
これはUnlabeledの中に存在する、PositiveとNegativeのサンプルのlossの値。

Negativeは一貫して減少しているが、これはNegative Assumptionによって過剰にNegativeだと分類されてしまうからである。

Positiveは最初は、Resamplingを繰り返した各セットでそれを学習させるので、うまくPositiveの特徴をつかむまで時間がかかる。だからPositiveのErrorは最初は上がったりする。ただし、epochが進むと必ず一筋縄に下がるとは限らない。Negative Assumptionによって過剰にNegativeに分類されて上がってしまうとErrorが上がり、ちゃんと学習ができているとErrorが下がる。これらが複雑に混ざり合うので、傾向が全然違う動きになる。

この論文ではTrend予測として、Mann-Kendall Testという手法でトレンドを見た。

データは全部Uniqueでランク付けでき、時系列データだとする。データ $x_i$について、 $[i+1, T]$までのすべてのデータと比べて、値が大きければ＋1、小さければ-1、同じなら0とする。全部で $T(T-1)/2$回比較し、その和を $S$とする。ここから次の式でZスコアを算出。

Sが正なら

Sが負なら

Sが0ならば0。

この $Z$が標準正規分布におけるp値(この論文では $\gamma$)について、十分に小さい or 大きい(有意水準以下)だと、トレンドが存在するというと考えられる。

今回の論文はこれでTrendをはかり、1. Negativeは減少している。 2. Positiveは増加かTrendなしかの半々。という結果に

Mann-Kendallテストとんちエイルように、次のような式で定義される量は傾向として扱うのに重要である。

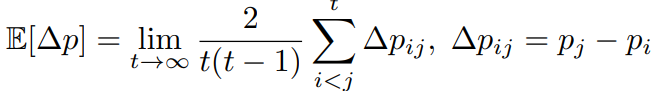
実際は有限のiterationなので、以下のような推定値となる。

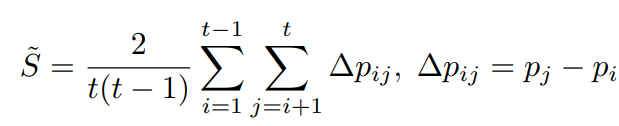
ただし、これは外れ値に弱い、ガウス分布に従わないデータの出現に弱いという問題がある。改善策としては以下のような改造がある。 $\alpha$は0以上。

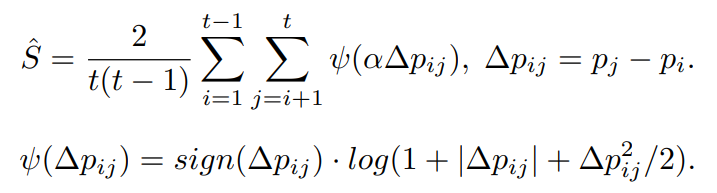
これは、以下の文献から得ている。

X. Xia, T. Liu, B. Han, M. Gong, J. Yu, G. Niu, and M. Sugiyama. Sample selection with
uncertainty of losses for learning with noisy labels. arXiv preprint arXiv:2106.00445, 2021.

K. H. Hamed and A. R. Rao. A modified mann-kendall trend test for autocorrelated data.
Journal of hydrology, 204(1-4):182–196, 1998.

この章では、Trendの評価についての説明である。

Unlabeledのデータからいくつかの各進度が高いデータを見つけ出すのはPUにおいては、sample-selection methodと言われている。